Properties of a parallelogram
A quadrilateral is a plane geometric figure that has four sides and four vertices. If in such a quadrilateral, both the pairs of the two opposite sides are parallel and they are also congruent to each other, then such a quadrilateral is called a parallelogram. (Abbreviated as ||gm). The figure below shows a sample parallelogram.

In the above picture, ABCD is a parallelogram. The two sides AB and DC are parallel to each other. This is indicated by the single arrows. The other two sides AD and BC are also parallel to each other. This is indicated by double arrows on both the sides. Also the length of the side AB is same as that of DC and the length of the side AD is same as that of BC. The four angles of the parallelogram are:Properties of parallelogram:
1. The first property we already stated in the definition of the parallelogram, that the opposite sides are parallel to each other.
2. The opposite sides are also congruent to each other. This we saw in the figure above and its description.
3. The opposite angles are congruent. Thus in the above figure,
4. The adjacent angles are supplementary. Thus in the above figure:
mmmm
5. The diagonal of a || gm divide the || gm into two congruent triangles. This can be shown with the help of the following figure:

In the above figure, ABCD is a || gm. AC is its diagonal. Now if we consider the triangles DAC and BAC, we see that one of the sides AC is common to both the triangles. We already established as the property number 2 of the || gm that the opposite sides are congruent. Therefore the side DC is congruent to AB and DA is congruent to CB. Therefore by the SSS congruency theorem, the two triangles DAC and BAC are congruent. Hence the property 5 of the || gm stands proved.
6. Area of a parallelogram: Since we just established that the diagonal of the parallelogram divides the || gm into two congruent triangles, if we know the area of one of these triangles we can find the area of the || gm by doubling the area of the triangle. Let us now see how to find the area of the || gm.
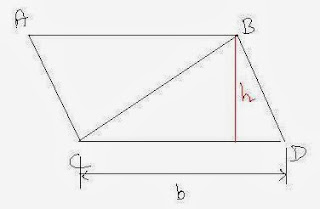
Consider the || gm ABCD shown in the figure below:
The triangle BDC has the length of base = DC = b and the altitude = h. The area of this triangle is therefore given by the formula:
∆ =(1/2)*base*height
∆ =(1/2)* b*h
Now we already established that the area of the || gm is twice the area of this triangle. Thus the area of the | | gm ABCD would be:
A=2* ∆
A=2*(1/2)* b* h
A=b*h
Properties of normal distribution is a topic of statistics and therefore shall be tackled under a separate article.
A quadrilateral is a plane geometric figure that has four sides and four vertices. If in such a quadrilateral, both the pairs of the two opposite sides are parallel and they are also congruent to each other, then such a quadrilateral is called a parallelogram. (Abbreviated as ||gm). The figure below shows a sample parallelogram.
In the above picture, ABCD is a parallelogram. The two sides AB and DC are parallel to each other. This is indicated by the single arrows. The other two sides AD and BC are also parallel to each other. This is indicated by double arrows on both the sides. Also the length of the side AB is same as that of DC and the length of the side AD is same as that of BC. The four angles of the parallelogram are:
1. The first property we already stated in the definition of the parallelogram, that the opposite sides are parallel to each other.
2. The opposite sides are also congruent to each other. This we saw in the figure above and its description.
3. The opposite angles are congruent. Thus in the above figure,
4. The adjacent angles are supplementary. Thus in the above figure:
m
5. The diagonal of a || gm divide the || gm into two congruent triangles. This can be shown with the help of the following figure:
In the above figure, ABCD is a || gm. AC is its diagonal. Now if we consider the triangles DAC and BAC, we see that one of the sides AC is common to both the triangles. We already established as the property number 2 of the || gm that the opposite sides are congruent. Therefore the side DC is congruent to AB and DA is congruent to CB. Therefore by the SSS congruency theorem, the two triangles DAC and BAC are congruent. Hence the property 5 of the || gm stands proved.
6. Area of a parallelogram: Since we just established that the diagonal of the parallelogram divides the || gm into two congruent triangles, if we know the area of one of these triangles we can find the area of the || gm by doubling the area of the triangle. Let us now see how to find the area of the || gm.
Consider the || gm ABCD shown in the figure below:
∆ =(1/2)*base*height
∆ =(1/2)* b*h
Now we already established that the area of the || gm is twice the area of this triangle. Thus the area of the | | gm ABCD would be:
A=2* ∆
A=2*(1/2)* b* h
A=b*h
Properties of normal distribution is a topic of statistics and therefore shall be tackled under a separate article.
No comments:
Post a Comment