Definition: A circle is a collection of all points in a plane which are at a constant distance (radius) from a fixed point (centre). Properties of a circle encompass use of terms such as chord, segment, sector, diameter etc of a circle. Now let us try to understand some other terms related to properties of circles.
Properties of circle:
A straight line that intersects a circle in two distinct points is called a secant to that circle. In the picture below, we have a circle with centre at C. A line l intersects this circle in two points, A and B. This line is a secant to the circle.
Circle theorems:
1. The tangent at any point of a circle is perpendicular to the radius through the point of contact. This we can see in the above picture. The tangent is perpendicular to the radius that joins the point of contact with the centre of the circle.
2. The lengths of tangents drawn from an external point to a circle are equal.
Circle formulas geometry:
Area of a circle: Area of a circle is given by the formula:
A = pi r^2
Area of semi circle: Area of a semi circle of radius r is given by the formula:
A = (pi/2)r^2
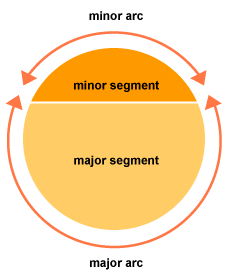
Segment of a circle:
The portion (or part) of the circular region enclosed between a chord and the corresponding arc of the circle is called a segment of the circle.
In the picture above, the orange portion is called the minor segment of the circle and the yellow portion is the major segment of the circle. The minor segment corresponds to minor arc and the major segment corresponds to the major arc of a circle.
Area of a segment of a circle is found using the formula below:
Where, theta is the angle subtended by the chord at the centre of the circle and r is the radius of the circle.
No comments:
Post a Comment