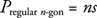Regular Polygons

Let us learn about Regular Polygons,
There is really no limit to the number of sides a polygon may have. The only practical limit is that unless you draw them on a very large sheet of paper, after about 20 sides or so, the polygon begins to look very much like a circle.

Parts of a regular polygon
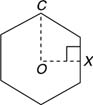
In a regular polygon, there is one point in its interior that is equidistant from its vertices. This point is called the center of the regular polygon. In Figure 1, O is the center of the regular polygon.

Figure 1 Center, radius, and apothem of a regular polygon.

The radius of a regular polygon is a segment that goes from the center to any vertex of the regular polygon.

The apothem of a regular polygon is any segment that goes from the center and is perpendicular to one of the polygon's sides. In Figure 1 , OC is a radius and OX is an apothem.

Finding the Perimeter

Because a regular polygon is equilateral, to find its perimeter you need to know only the length of one of its sides and multiply that by the number of sides. Using n-gon to represent a polygon with n sides, and s as the length of each side, produces the following formula.

Finding the Area

If p represents the perimeter of the regular polygon and a represents the length of its apothem, the following formula can eventually be shown to represent its area.

Example 1: Find the perimeter and area of the regular pentagon in figure 2 , with apothem approximately 5.5 in.

Figure 2

Finding the perimeter and area of a regular pentagon.

Hope the above explanation helped you.