Let us learn about perimeters and areas of similar triangles,
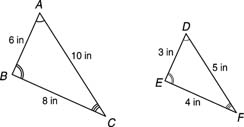
When two triangles are similar, the reduced ratio of any two corresponding sides is called the scale factor of the similar triangles. In Figure 1 , Δ ABC∼ Δ DEF.
The ratios of corresponding sides are 6/3, 8/4, 10/5. These all reduce to 2/1. It is then said that the scale factor of these two similar triangles is 2 : 1.
The perimeter of Δ ABC is 24 inches, and the perimeter of Δ DEF is 12 inches. When you compare the ratios of the perimeters of these similar triangles, you also get 2 : 1. This leads to the following theorem.
Theorem : If two similar triangles have a scale factor of a : b, then the ratio of their perimeters is a : b.
Hope the above explanation helped you.
When two triangles are similar, the reduced ratio of any two corresponding sides is called the scale factor of the similar triangles. In Figure 1 , Δ ABC∼ Δ DEF.
| |||
| |||
The perimeter of Δ ABC is 24 inches, and the perimeter of Δ DEF is 12 inches. When you compare the ratios of the perimeters of these similar triangles, you also get 2 : 1. This leads to the following theorem.
Theorem : If two similar triangles have a scale factor of a : b, then the ratio of their perimeters is a : b.
Hope the above explanation helped you.