Basics about Circles

Definition: A circle is a collection of all points in a plane which are at a constant distance (radius) from a fixed point (centre). Properties of a circle encompass use of terms such as chord, segment, sector, diameter etc of a circle. Now let us try to understand some other terms related to properties of circles.

Properties of circle:
A straight line that intersects a circle in two distinct points is called a secant to that circle. In the picture below, we have a circle with centre at C. A line l intersects this circle in two points, A and B. This line is a secant to the circle.

A straight line that intersects (or touches) a circle in just one point is called a tangent to the circle at that point. For a circle at a given point, there can be only one tangent. The tangent to a circle is a special case of the secant, when the two end points of its corresponding chord coincide. See picture below.

Circle theorems:

1. The tangent at any point of a circle is perpendicular to the radius through the point of contact. This we can see in the above picture. The tangent is perpendicular to the radius that joins the point of contact with the centre of the circle.

2. The lengths of tangents drawn from an external point to a circle are equal.

Circle formulas geometry:

Area of a circle: Area of a circle is given by the formula:
A = pi r^2
Area of semi circle: Area of a semi circle of radius r is given by the formula:
A = (pi/2)r^2

Segment of a circle:

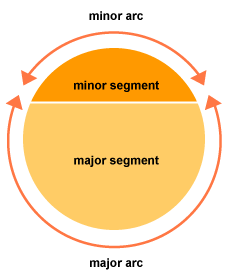
The portion (or part) of the circular region enclosed between a chord and the corresponding arc of the circle is called a segment of the circle.

In the picture above, the orange portion is called the minor segment of the circle and the yellow portion is the major segment of the circle. The minor segment corresponds to minor arc and the major segment corresponds to the major arc of a circle.

Area of a segment of a circle is found using the formula below:

Where, theta is the angle subtended by the chord at the centre of the circle and r is the radius of the circle.

Calculate Time - Fourth Grade Math

In grade four, new concepts are introduced in math. Some new concepts are time, multiples and factors, addition and subtraction of three digit numbers, unitary method, measures of length, mass and capacity, fractional numbers, addition and subtraction of fractions, decimals, addition and subtraction of decimals, Introduction to angles.

Introduction to grade four math:

In grade four, the topic time contains the following sub units.

- Measurement of time

-Calender

- Time in second

- Addition and subtraction of time

In this article let us learn about 24-hour clock time.

In the present day world business houses, airlines, railways are busy round the clock. Hence it is convenient to use 24 - hour time representation instead of a.m. and p.m.

1. 12 O' clock midnight is expressed as 00 00 or 24 00

2. 12 O' clock is expressed as 12 00

3. The time between 12 O' clock noon and 12 O' clock midnight is expressed by adding 12 hours to the given hours period.

For example:

25 minutes past 6 in the evening is expressed as 18 25

45 minutes past 11 midnight is written as 23 45

Rules for Writing 24-hour Clock Time:

A day begins at 12 midnight (00:00 hours) and hence at 12 midnight the following day.

Thus 1 day = 24 hours

Rule 1: For any time in a.m. we simply put down the time by writing hours and minutes in two digits numbers.

Rule 2: For any time written in p.m. we simply add 12 hours to the number of hours period and write minutes without separating them.

6:25 a.m is written as 06 25 hours

10:45 a.m is written as 10 45 hours

3:10 p.m. is written as 15 10 hours (3 + 12 = 15)

10:50 p.m. is written as 22 50 hours (10 + 12 = 22)

Example Problems on Grade Fourth Math:

Ex 1: Express 11:25 p.m. in the 24 hours system.

Sol:

Step 1: See which rule can be used.

Step 2: Since the time given is in p.m., add 12 to 11

Step 3: So, 11:25 p.m. = (11 + 12 hours) : 25 min

= 23 25 hours

Ex 2: Express 18 30 hours in terms of a.m. or p.m.

Sol:

18 30 hours means (12 + 6 hours) 30 minutes

= 6:30 p.m.

Ex 3: Express 07:45 p.m. in the 24 hours system.

Sol:

Step 1: See which rule can be used.

Step 2: Since the time given is in p.m., add 12 to 7

Step 3: So, 07:45 p.m. = (7 + 12 hours) : 45 min

= 19 : 45 hours

Trigonometric Integrals

Trigonometry is a fundamental concept of mathematics. It is used in calculus functions and vectors. In this topic we have to use trigonometry as integral function. That means how to integrate trigonometric functions. For this we also have to know what is integration?  Integration means to calculate area of a given curve, and the curve is a closed curve made by x axis and y axis.

Trigonometric integrals mean integration of trigonometric functions. As we know these trigonometric functions are basic formulas for solving trigonometric integral. To more simplify this term, let’s take an example like sin2X. This is a trigonometric function. And we integrate this function for this first we have to expand this term by using formula of trigonometry. After expanding we carry out the constant term then by using product rule of integral, we can integrate this trigonometric function.

Above example is simple it has only one trigonometric function but trigonometric function may be combine with other function also. It can be algebraic function with trigonometry, logarithmic function with trigonometry and exponential function with trigonometry. These are also called integrals of trigonometric functions. To solve this type of problem either we can use integration by substitution method or integration by parts method.

Inverse trigonometric integrals such as sin^-1X and cos ^-1X etc. now to integrate this type of functions we have to use basics of calculus. We need  to take this function equal to any constant like Y. means we have to write Y= sin ^-1X. now we transfer sin function to other site the we get. X=sin Y. Now we can simply integrate this term.

Trigonometric substitution integrals, here we also integrate trigonometric functions and calculus functions, but procedure is different. To integrate this type of function we have to substitute and equal trigonometric term in place of other trigonometric term. The first from of integrals is integration of [f’(x)/f(x)] dx=logf(x) . In this form integral of a function whose numerator is the exact derivative of its denominator and equal to the logarithmic of its denominator? The second form is, in the integrand consist of the product of a constant power of a function f(x) and the derivative of f(x), to obtain the integral we increase the index by unity and then divide by increase index. This procedure is known as power formula. Lets take an example suppose we have to integrate (4x^3/1+x^4) dx= ln (1+x^4). By using this method we substitute 1+x^4 = any constant term like (t), and after that we integrate this function.

Exponential Function an Introduction

An Exponential Function is a function which involves exponent which is the variable part rather than the base as in any normal function. For instance f(x)= x^3 is a function and an exponential function is something like g(x)= 3^x, here the exponent or the power is a variable (x) and the fixed value is the base (3). So, the definition of Exponential functions can be given as a function whose base is a fixed value and the exponent a variable. Example: f(x) = 5^x, here the base 5 is fixed value and the exponent ‘x’ is the variable.
In general, we can define Exponential Functions as a function which is written in the form ‘a^x’ in which ‘a’ is the base which is a fixed value or constant (‘a ‘not equal to 1) and ‘x’ the variable which is any real number. The most common exponential function we come across in math is e^x which is known as the Euler’s number.
Let us now take a quick look at the Exponential Function Properties. Consider the Exponential function f(x) = b^x for which the properties are as follows:
• The domain of the exponential function consist of all real numbers
• The range is the collection of all positive real numbers
• When b is greater than 1 then the function is an increasing function also called exponential growth function and when b is less than 1 then the function is a decreasing function also called exponential decay function
• The other properties that an exponential function satisfy are,
1. b^x.b^y = b^(x+y) [when bases are same and a multiplication operation then we can add the powers]
2. b^x/b^y = b^(x-y)[when bases are same and a division operation then we can subtract the powers]
3. (b^x)^y = b^(xy) [when a base is raised to a power x and raised to whole power y then we can multiply the powers]
4. a^x.b^x= (a.b)^x [when bases are different with the same power and a multiplication operation then we can multiply the bases whole raised to power]

We come across a function called an Inverse Exponential Function; this is nothing but a logarithm function.  We know that the exponential function is written in the form f(x) = b^x, to find the inverse of a given function we need to interchange x and y and solve for y. By interchanging we get x = b^y  and then solving for y gives us y = log x (base b) which is a logarithm function.

Points and lines tutoring

Tutor is the person who teaches the kids and this teaching section is the tutoring. Tutoring is an open source for the students to gain knowledge that is in online a point is nothing but the dot , it has no dimension or no width, it’s only a simple black dot. In geometry co ordinates of a point which shows the particular place in a segment for representation.Line has two end points is called segment. Line segment is denoted with a connected piece of line.line segments names  has two endpoints and it is named by its endpoints.

Points and Lines Tutoring:

Tutoring about the geometric points and lines we have to know the classification of a points and lines. points and lines classification are as follows.

Collinear points:
When three or more points lies on the same line is said to be collinear points.

Midpoint:
A halfway point where line segment divides into two equal parts are called midpoint.

Equidistant point:
A point which is said to be equidistant in a line segment where point is equal length from other points which are in congruent then the point is equidistant point.

Parallel line segment:
Two lines which does not touch each other are called parallel lines.

Perpendicular line segment:
Two line segment  that form a L shape are called perpendicular lines.

Problems in Points and Lines Tutoring:

Example 1:
Find the distance between the points A(6,3) and B (2,1).

Solution:
Let assume "d" be the distance between A and B.           (x1,y1)= (6,3), (x2,y2)= (2,1).

Then d (A, B) =`sqrt((x_2-x_1)^2+(y_2-y_1)^2)`

= `sqrt((2-6)^2 +(1-3))^2)`

= `sqrt((-4)^2+(-2)^2)`

= `sqrt(16+4)`

=`sqrt20`
=2`sqrt5`

Example 2:
Find co-ordinate of the mid point of the line segment joining given points A(-5,3) and B(2,1)

Solution:
The required mid point is
Formul a   `((x_1+x_2)/2 ,(y_1+y_2)/2)` here,  (x1, y1) = (-5,3),(x2, y2) = (2,1)

=  `((-5+2)/(2))``((3+1)/(2)) `

=   `(-3/2) ` , ` (4/2)`

=    `(-3/2, 2)`

Example 3:
Find the slope of the lines given (8,-5) and (4,2)

Solution:
(x1,y1)= (8,-5), (x2,y2)= (4,2).
We know to find slope of line,m=` (y_2-y_1) /(x_2-x_1)`

=`(2+5)/(4-8)`

m =`7/-4`

Example 4:
Find the equation of the line having slope  3 and y-intercept 5.

Solution:
Applying the equation of the line is y = mx + c
Given,       m =3 ,c = 5
y =  3x +5

or  y = 3x+5
or  -3x+y-5 = 0
3x-y+5 = 0.